طريقة تدريس المساحه وقياسها نموذجيا وشكرا
حتى انا اريد
تحضير وطريقة الشرح والمقدمة اهم شي ياعالم احتاج مقدمة اي تهئية للدرس ضرووووووووري
اللهم صلي وسلم على نبينا محمد
سبحان الله وبحمده سبحان الله العظيم
لاحول ولاقوة الابالله
سبحان الله وبحمده عدد خلقة ورضى نفسة وزنة عرشة ومداد كلماته
لا اله الا الله وحده لاشريك له له الملك وله الحمد وهو على كل شي قدير
استغفر الله العظيم واتوب اليه
أولاً :حساب مساحة المستطيل والمربع عند حساب مساحة مستطيل كالشكل التالي نعني حساب المنطقة المحصورة داخل أضلاع المستطيل فلو قسمنا المستطيل إلى مربعات متطابقة . بحيث يكون طول كل مربع منها ( 1 سم) فستجد أن هناك (18) مربعاً متطابقة . وستكون هذه المربعات المتطابقة عبارة عن حاصل ضرب ( 6 مربعات ) في الطول و (3) مربعات في العرض .
نستطيع القول أنمساحة المستطيل=الطول ( سم )× العرض (سم) =المساحة سم2

أمثلة :
1.ما مساحة المستطيل الذي طوله ( 4 سم ) وعرضه ( 3سم ) .
الحل : المساحة للمستطيل = الطول × العرض = 4 × 3 = 12 سم2 وتقرأ سم مربع
2.قطعة أرض مستطيلة الشكل طولها 45 م وعرضها 23 م أوجد مساحتها .
الحل : مساحة الأرض = الطول × العرض
= 45 × 23 = 1035 م2 .
3.نافذة طولها = 2 م ، وعرضها 3 م احسب مساحة الزجاج اللازم لإغلاقها .
مساحة الزجاج = 2 × 3 = 6 م2 .
مساحة المربع : المربع هو مستطيل تساوى طوله مع عرضه .
إذنمساحته = طول ضلعه × طول ضلعه أي تساوي مربع طول ضلعه من الوحدات المربعة .
الخلاصة :عند حساب مساحة المستطيل أو المربع تذكر القانون

مساحة المستطيل = الطول × العرض = وحدة مربعة .

مساحة المربع = ( الضلع )2 = وحدة مربعة .
ثانياً : حساب مساحة متوازي الأضلاع :
انظر الشكل المجاور إنه يتكون من المستطيل هـ ع ك ل ، ومتوازي الأضلاع و ع ك م.
ما الشيء المشترك بين المستطيل ومتوازي الأضلاع ؟
الجواب إنه القاعدة —– إنهما أيضاً محصوران بين مستقيمين
متوازيين هما القاعدة المشتركة ع ك والمستقيم هـ م .
لاحظ في الرسم أيضاً وجود شكل شبه منحرف هو و ع ك ل وهو قسم مشترك أيضاً بين المستطيل ومتوازي الأضلاع.
لاحظ أنه يوجد في الشكل مثلثان هما هـ ع و ، ل ك م وليس من الصعب عليك أن تستنتج أنهما متطابقان تماماً ( ابحث في هذا الأمر بنفسك ) .
لاحظ الآن أن المستطيل = rهـ ع و + شبه المنحرف و ع ك ل ……..(1)
وأن متوازي الأضلاع =rل ك م + شبه المنحرف و ع ك ل ……..(2)
أن الطرف الأيسر من المعادلتين 1 ،2 متساو لأن rهـ ع و =rل ك م ، ولأن شبه المنحرف و ع ك ل موجود في كل منهما .
إذن الطرف الأيمن في كلا المعادلتين متساو وهذا من البديهيات . أكمل نص البديهية المؤدية إلى هذه النتيجة وهي :
الشيئان المساويان لثالث ———— .
إذن مساحة المستطيل هـ ع ك ل = مساحة متوازي الأضلاع و ع ك ل .
لكن مساحة المستطيل = ع ك × ك ل
إذن مساحة متوازي الأضلاع و ع ك ل = ع ك × ك ل
إن ع ك هي قاعدة متوازي الأضلاع ، أما ك ل فهو ارتفاعه
تعريف : ارتفاع متوازي الأضلاع : هو العمود النازل من أحد الرؤوس على القاعدة المقابلة ، إذن مساحة متوازي الأضلاع و ع ك ل = طول قاعدته × طول ارتفاعه
وباختصار=القاعدة × الارتفاع
ينطبق هذا الأمر على أي متوازي أضلاع آخر لذلك نقول عموماً :
مساحة متوازي الأضلاع = طول قاعدته × طول ارتفاعه .
أمثلة :احسب مساحة كل من الأشكال التالية :
شكل (1)

مساحة الشكل (1) = طول القاعدة × الارتفاع
= 8 × 3 = 24 سم2 .
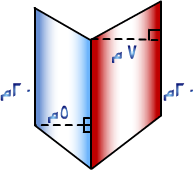
مساحة الشكل (2) = مساحة متوازي الأضلاع الأحمر + متوازي الأضلاع الأزرق
مساحة متوازي الأضلاع الأحمر = 20 × 7 = 140 م2 .
مساحة متوازي الأضلاع الأزرق = 5 × 20 = 100 م2 .
مساحة الشكل = 140 + 100 = 240 م2 .

تدريب شفوي :
أجب عن التمارين الآتية شفهياً :
ـ ما مساحة متوازي أضلاع طول قاعدته 10 سم وارتفاعه 5 سم .
ـ ما مساحة متوازي أضلاعه الذي طول ارتفاعه 20 م وطول قاعدته 7 م .
ـ قطعة أرض على شكل متوازي أضلاع طول قاعدته 100 م وارتفاعه 60 م ، أوجد مساحتها .
ـ متوازي أضلاعه مساحته 450 م2 وارتفاعه 9 م ، ما طول قاعدته .
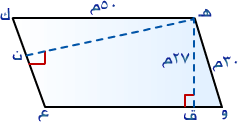

تدريب (2) :
الشكل هـ و ع ك متوازي الأضلاع والأبعاد ظاهرة عليه ، احسب طول هـ ن .
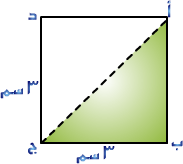
تعلمت أن مساحة المربع هي طول ( الضلع )2 فلو كان لدينا مربع طول ضلعه 3سم كما في الشكل وطلب منك إيجاد مساحته لكان جوابك هو ( 9 سم2) .
ما مقدار مساحة المثلثأ ب جـ مقارنة بمساحة المربع أ ب جـ د .

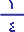

أ ب جـ =
×(الضلع)2

مساحة المستطيل .
 أ ب جـ =rوكذلك الأمر لو كان بدلاً من المربع مستطيل فإن مساحة
أ ب جـ =rوكذلك الأمر لو كان بدلاً من المربع مستطيل فإن مساحة

× 3 × 2 = 3 سم 2 × الطول × العرض =
× الطول × العرض =
 =
=
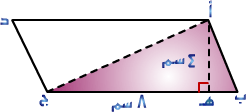
وأيضاً لو طلب إيجاد مساحة r أ ب جـ في الشكل المجاور .
لاحظ أن rأب جـ عبارة عن نصف متوازي الأضلاعأب جـ د
مساحة متوازي الأضلاعأ ب جـ د

أ ب جـ =
× (طول القاعدة × الارتفاع )

=×32 = 16 سم2.

(8×4)=

=
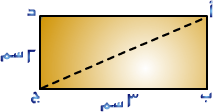
نلاحظ مما سبق أن مساحة المثلث هي عبارة عن نصف مساحة المستطيل أو المربع أو متوازي الأضلاع وهذا يقودنا إلى استنتاج مفاده أنّ :
×طول القاعدة × الارتفاع

مساحة المثلث=

نشاط للدارس :
أثبت أن مساحة أي متوازي أضلاع = حاصل ضرب قاعدته × ارتفاعه وذلك عن طريق توصيل أحد قطريه .
× ارتفاعه
× قاعدته

على أساس أن مساحة المثلث =

أمثلة :احسب مساحة كل من المثلثات التالية :
جبأ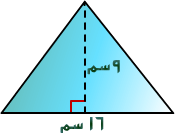

× ارتفاعه
× قاعدته

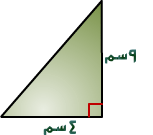
مساحة المثلث(أ)
× 6×2 = 6 سم2.
لاحظ هنا الارتفاع كان (2) وليس (4) لأن الارتفاع يجب أن يكون عمودياً على القاعدة .
×4×9 = 18 سم2.

مساحة المثلث(ب)
×(حاصل ضرب ضلعي القائمة)
 لاحظ في المثلث القائم الزاوية تكون المساحة =
لاحظ في المثلث القائم الزاوية تكون المساحة =
×16×9 = 72 سم2.
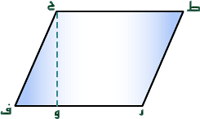
رابعاً:مساحة المعيَّن :
من منطلق كون المعيَّن متوازي الأضلاع ( لكن أضلاعه الأربعة متساوية )
إذن…..
مساحته=قاعدته ×ارتفاعه
= طول أحد أضلاعه×ارتفاعه(العمود النازل عليه من الرأس المقابل)
في الشكل المعطى مساحة المعين=ر ف×ح و
حيث رف يمثل طول ضلع —– ، ح ويمثل ارتفاعه .
طريقة أخرى لحساب مساحة المعيَّن : هل تتذكر خواص قطري المعيَّن؟ أولاً :ينصف كلاً منهما الآخر أي أنّ : ي م = م ل
وكذلكح م = —–
ثانياً :متعامدان أي أن الزوايا الأربع التي رأسها م كلها قوائم .
وعلى هذا الأساس في المثلث ح ي ل، يمكن اعتبار ي ل قاعدة،ح م الارتفاع .
مساحة المعيَّنح ي ن ل

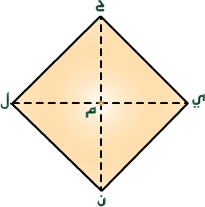
مساحة المثلث ح ي ل
2×
أي أن مساحة المعيَّنح ي ن ل=
ي ل × ح م

2×
ي ل × ح م
ح ن) .

(ح م =

ي ل×


× حاصل ضرب قطريه .

مساحة المعيَّن=
الخلاصة :

حل التمارين التالية شفوياً : أ.جد مساحة المعيَّن الذي طول ضلعه 10 م وارتفاعه 6 م .
ب.جد مساحة المعيَّن حيث طولا قطريه 20 ، 15 م .
ج.مساحة المعيَّن100 سم2 وطول أحد قطريه 20 سم ، أوجد طول القطر الثاني .
تعلم أن شبه المنحرف هو شكل رباعي فيه ضلعان متوازيان فقط ، نطلق على هذين الضلعين المتوازيين اسم
القاعدتين وكل ضلع منهما قاعدة .كيف نجد مساحة شبه المنحرف بالاستفادة من هاتين القاعدتين المتوازيتين ؟
انظر الأشكال التالية لتساعدك في معرفة كيفية حساب مساحة شبه المنحرف .
شكل (2)
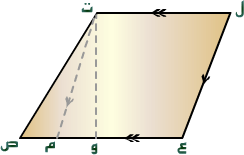
شكل (1)
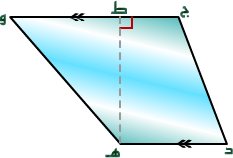
ـفي الشكل(1)— العمود النازل من الرأس على القاعدة المقابلة لشبه المنحرف يسمى ارتفاع شبه المنحرف ، قاعدتا شبه المنحرف هما د هـ ، ج و .
د هـ ط
قائمة( ما الدليل على ذلك ؟) .
ـفي الشكل(2)—ل ع ص تشبه منحرف قاعدتاه المتوازيتان همال ت ، ع ص ، أما ارتفاعه فهوت و.
أمات مفقد رسمناه موازياً لضلع شبه المنحرفل ع .

ما نوع الشكل ل ع م ت ؟ إنه متوازي الأضلاع ( ما الدليل على ذلك ؟) .
لقد انقسم شبه المنحرف بالخط ت م إلى قسمين هما متوازي الأضلاع ل ع م ت ، والمثلث ت م ص .
شبه المنحرف ل ع ص ت= متوازي الأضلاعل ع م ت+ المثلثت م ص
مساحة شبه المنحرف ل ع ص ت=مساحة متوازي الأضلاع ل ع م ت + مساحة المثلث ت م ص

والآن كيف نحسب مساحة متوازي الأضلاع ل ع م ت ؟
مساحة متوازي الأضلاع ل ع م ت = قاعدته × ارتفاعه
= ع م × ت و ………………..(1)
= ل ت × ت و لأن ع م = ل ت
…………………….(2)
× م ص × ت و
